Aufgaben
Inhaltsverzeichnis
\(\\\)
“Gehwegplatte”
Eine dekorativ geschwungene Gehwegplatte wird untersucht. Wird die Gewegplatte von oben betrachtet, hat sie die in der Abbildung 1 dargestellte Form.

\(\\\)
Diese Form ist symmetrisch bezüglich der \(x\)-Achse des eingezeichneten Koordinatensystems.
Der obere Rand der Form wird beschrieben mithilfe des Graphen der Funktion \(f\) mit
\(\quad f(x) \; = \; -\frac{3}{250} \cdot x^4 + \frac{18}{125} \cdot x^3 - \frac{54}{125} \cdot x^2 + 2 \quad \textit{und} \quad 0 \leq x \leq 6 \)
\(\\\)
Eine Längeneinheit entspricht einen Dezimeter in der Wirklichkeit.
\(\\[2em]\)
Untersuchung der Kontur
- Berechnen Sie die Koordinaten des Tiefpunktes des Graphen von \(f\).
(4 P)
\(\\\)
-
Zeichnen Sie den Graphen von \(f\) in die Abbildung 2 ein.

\(\qquad \qquad \qquad\)(3 P)
\(\\\)
-
Die Breite der Form an jeder Stelle \(x\) mit \(x \in [0;6]\) ist \(2 \cdot f(x)\). Es gibt \(2\) Stellen \(x \in [0;6]\), an denen die Form eine Breite von \(3\) Längeneinheiten aufweist.
Bestimmen Sie den Abstand dieser beiden Stellen voneinander.
(3 P)
\(\\[2em]\)
Der linke Rand der Form wird oberhalb der \(x\)-Achse modelliert mithilfe des Graphen der Funktion \(l\) mit
\(\quad l(x) \; = \; 2 \cdot (x + 1) \cdot e^{-0{,}73 x} \quad \textit{und} \quad -1 \leq x \leq 0 \)
\(\\[1em]\)
Maßzahlen der Gehwegplatte
Der rechte Rand der Form wird mithilfe einer Funktion \(r\) modelliert. Der Graph von \(r\) ergibt sich durch eine Verschiebung des Graphen von \(l\) entlang der \(x\)-Achse und ist über dem Intervall \([5;6]\) in der obigen Abbildung 2 dargestellt.
\(\\\)
- Leiten Sie einen Funktionsterm von \(r\) her.
(2 P)
\(\\\)
-
Begründen Sie, dass der Flächeninhalt der Form mit dem Term
\(\quad 2 \cdot \displaystyle{\int}_0^6 f(x) \, dx \)
berechnet werden kann.
(3 P)
\(\\\)
-
Ein Kubikdezimeter des zur Herstellung der Gehwegplatten verwendeten Materials hat eine Masse von \(1{,}76 \, kg\).
Berechnen Sie die Masse einer Gehwegplatte mit einer Plattendicke von einem halben Dezimeter.
(4 P)
\(\\\)
-
Die Bogenlänge \(L\) des Graphen einer differenzierbaren Funktion \(h\) über einem Intervall \([a;b]\) lässt sich berechnen durch
\(\quad L \; = \; \displaystyle{\int}_a^b \sqrt{1 + \big( h'(x) \big)^2} \, dx \)
Berechnen Sie mithilfe dieser Formel den Umfang der Form.
(4 P)
\(\\[2em]\)
Winkel und Tangente
-
Der linke und der obere Rand der Form treffen im Punkt \((0 | 2)\) in einem Winkel \(\alpha\) aufeinander. Die Situation ist in der Abbildung 3 dargestellt.
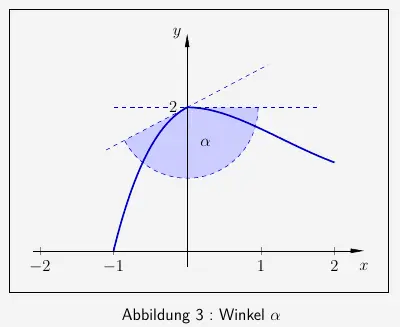
Berechnen Sie \(\alpha\).
(3 P)
\(\\\)
-
Die Gerade \(g\) verläuft durch den Punkt \(P(0 | 2)\) und ist orthogonal zur Tangente an den Graphen von \(l\) im Punkt \(P\).
Berechnen Sie den Schnittpunkt von \(g\) mit der \(x\)-Achse.
(4 P)
\(\\[2em]\)
Funktionenschar
Betrachtet wird nun die Schar der in \(\mathbb{R}\) definierten Funktionen \(f_k\) mit
\(\quad f_k(x) \; = \; -\frac{1}{100} k \cdot x^4 + \frac{3}{25} k \cdot x^3 - \frac{9}{25} k \cdot x^2 + 2 \quad \textit{und} \quad k \not= 0 \)
\(\\[1em]\)
-
Berechnen Sie de Wert \(k\), für den
\(\quad f_k(x) \; = \; f(x) \)
ist.
(2 P)
\(\\\)
-
Bestimmen Sie für jedes \(k \not= 0\) die Wendestellen von \(f_k\).
\(\quad \big[ \text{Kontrolle:} \quad x \, = \, -\sqrt{3} + 3 \quad \vee \quad x \, = \, \sqrt{3} + 3 \big] \)
(4 P)
\(\\\)
-
Die Wendepunkte der Graph der Funktionen \(f_k\) liegen oberhalb, unterhalb bzw. auf der \(x\)-Achse.
Untersuchen Sie diesbezüglich die Lage der Wendepunkte in Abhängigkeit von \(k\).
(4 P)
\(\\[2em]\)